Robotic Rover Modeling and Control

Hongbo Zhang

16 Robotic Rover Modeling and Control

Hongbo Zhang

1) Rover Motion Equations

As discussed in Chapter 1, robots have many applications, from autonomous driving, industrial applications, medicine delivery, and construction. Among them, robot navigation has important applications. To implement these applications, we need to understand the mechanisms, how they work, and the challenges associated with the implementation. For these applications, it is important to understand the plant of the robotics platform. Let us draw the vehicle navigation diagram.

The robotics can be simplified to a two-wheel system model. The front wheel uses Ackermann steering mechanisms shown in Figure 16.1 below. In this figure, $\delta$ is the steering angle. $\beta$ is the body slip angle (see below).

Within this model, $\theta$ represents the orientation (yaw angle) of the robot. $\theta$ represents the direction in which the robot is traveling relative to a fixed reference global coordinate system.

The body slip angle $\beta$ is the angle between the vehicle’s heading direction (the desired direction) and its actual velocity vector (the actual direction).

$\beta = \arctan\left(\frac{l_r \tan(\delta)}{L}\right)$

Where $l_r$ is the distance between the rear of the robot and the center of mass of the robot.

Puting together the robotics model, we obtain the following robotics state space. The state space include four state space variables: linear position x and y, angle $\theta$ , and linear velocity v. With these variables, we thus enable the linear and angular position control of the robot.

$\begin{pmatrix} \dot x \\ \dot y \\ \dot \theta \\ \dot v \end{pmatrix} = \begin{pmatrix} v \cos(\theta + \beta) \\ v \sin(\theta + \beta) \\ \frac{v \cos(\beta) \tan(\delta)}{L} \\ a \end{pmatrix}$

where:
$\beta$ is the body slip angle.
$L$ is the wheelbase of the vehicle.
$\delta$ is the steering angle.
$a$ is the acceleration.

Evidently, from the above matrix, we can find that the model consists of the following state variables.

$\mathbf{x} = \begin{pmatrix} x \\ y \\ \theta \\ v \end{pmatrix}$

Correspondingly, the input vector consists of the following variables.

$\mathbf{u} = \begin{pmatrix} \beta \\ \delta \\ a \end{pmatrix}$

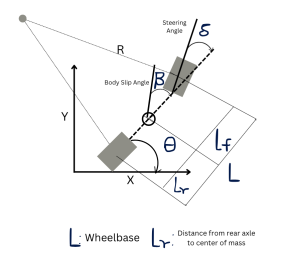
Robotics Rover — Figure 16.1: The diagram of the robotic rover.

In Figure 16.1, the diagram of the robotic rover:

$\beta$ is the body slip angle.
$L$ is the wheelbase length of the vehicle.
$\delta$ is the steering angle.
$l_r$ is the distance between the rear of the robot and the center of mass of the rover.

2) Rover State Space Linearization

It is also not difficult to find that the variables of $\dot x, \dot y, \dot \theta, \dot v$ are nonlinear. In order to proceed to model the system, we must first linearize the system so we can use linear control. For this purpose, we will linearize the system around an operating point and assume that the system operates at or near that point for the linearization to be valid. The operating point for this example is moving straight with a constant velocity $v_0$ . We also assume that the slip angle \beta = 0 around the operating point.

To linearize the system, we compute the Jacobian matrices of the state equations with respect to the state vector $\mathbf{x}$ and the input vector $\mathbf{u}$ . Remember that we assumed constant velocity $v_0$ and $\beta = 0$ .

Jacobian Matrix Example: First of all, what it is a Jacobian matrix? It is a partial derivative matrix. Chapter 4 explains this in detail, so please review that if you need a refresher. Then you can understand the simple example below.

For the following system of state equations:

$\begin{cases} \dot{x} = x^2 + y \\ \dot{y} = x + \sin(y) \end{cases}$

Here, the state vector is:

$\mathbf{x} = \begin{pmatrix} x \\ y \end{pmatrix}$

For the above equation, it is almost impossible to write its state space without transforming the two equations to different forms. Thus, the Jacobian matrix comes to save the situation via linearization.

For the above example, the Jacobian matrix $A$ of the two equations contains the partial derivatives of the state equations with respect to the state variables $x$ and $y$ .

Step 1: Partial Derivatives of $\dot{x}$ with respect to $x$ and $y$ :

$\begin{cases} \frac{\partial \dot{x}}{\partial x} = \frac{\partial (x^2 + y)}{\partial x} = 2x \\ \frac{\partial \dot{x}}{\partial y} = \frac{\partial (x^2 + y)}{\partial y} = 1 \end{cases}$

Partial derivatives of $\dot{y}$ with respect to $x$ and $y$ :

$\begin{cases} \frac{\partial \dot{y}}{\partial x} = \frac{\partial (x + \sin(y))}{\partial x} = 1 \\ \frac{\partial \dot{y}}{\partial y} = \frac{\partial (x + \sin(y))}{\partial y} = \cos(y) \end{cases}$

Step 2: Jacobian Matrix $A$ therefore becomes:

$A = \begin{pmatrix} \frac{\partial \dot{x}}{\partial x} & \frac{\partial \dot{x}}{\partial y} \\ \frac{\partial \dot{y}}{\partial x} & \frac{\partial \dot{y}}{\partial y} \end{pmatrix} = \begin{pmatrix} 2x & 1 \\ 1 & \cos(y) \end{pmatrix}$

As such, for the given system, the Jacobian matrix $A$ becomes:

$A = \begin{pmatrix} 2x & 1 \\ 1 & \cos(y) \end{pmatrix}$

3) Jacobian Matrix of the Rover Platform

Now that we have finished reviewing the basics of the Jacobian matrix, it is time for us to re-focus on calculating the Jacobian matrix $A$ . Before that, it is useful for us to review the robotics motion equation from above:

$\begin{pmatrix} \dot x \\ \dot y \\ \dot \theta \\ \dot v \end{pmatrix} = \begin{pmatrix} v \cos(\theta + \beta) \\ v \sin(\theta + \beta) \\ \frac{v \cos(\beta) \tan(\delta)}{L} \\ a \end{pmatrix}$

where:
$\beta$ is the body slip angle.
$L$ is the wheelbase of the vehicle.
$\delta$ is the steering angle.
$a$ is the acceleration

The Jacobian matrix $A$ is given by:

$A = \frac{\partial \mathbf{f}}{\partial \mathbf{x}} \bigg|_{(\mathbf{x}_0, \mathbf{u}_0)}$

For the above $\frac{\partial \mathbf{f}}{\partial \mathbf{x}}$ , $\partial \mathbf{f}$ refers to the partial derivative of the $\mathbf{f}$ . $\mathbf{f}$ refers to each element of the original matrix ( $\dot x, \dot y, \dot \theta$ , and $\dot v$ ). $\mathbf{x_0}, \mathbf{u_0}$ are the operating points of the robotics motion equation used to linearize the system.

Evaluating at the operating point 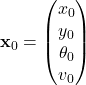$\mathbf{x}_0 = \begin{pmatrix} x_0 \\ y_0 \\ \theta_0 \\ v_0 \end{pmatrix}$ and $\mathbf{u}_0 = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}$ :

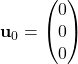$A = \begin{pmatrix} 0 & 0 & -v_0 \sin(\theta_0) & \cos(\theta_0) \\ 0 & 0 & v_0 \cos(\theta_0) & \sin(\theta_0) \\ 0 & 0 & 0 & \frac{\tan(\delta_0)}{L} \\ 0 & 0 & 0 & 0 \end{pmatrix}$

For the linearization operating point, we also assume $\delta_0 = 0$ :

$A = \begin{pmatrix} 0 & 0 & -v_0 \sin(\theta_0) & \cos(\theta_0) \\ 0 & 0 & v_0 \cos(\theta_0) & \sin(\theta_0) \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix}$

The Jacobian matrix $B$ is given by:

$B = \frac{\partial \mathbf{f}}{\partial \mathbf{u}} \bigg|_{(\mathbf{x}_0, \mathbf{u}_0)}$

Evaluating at the operating point 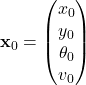$\mathbf{x}_0 = \begin{pmatrix} x_0 \\ y_0 \\ \theta_0 \\ v_0 \end{pmatrix}$ and $\mathbf{u}_0 = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}$ :

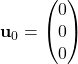$B = \begin{pmatrix} -v_0 \sin(\theta_0) & 0 & 0 \\ v_0 \cos(\theta_0) & 0 & 0 \\ 0 & \frac{v_0}{L} & 0 \\ 0 & 0 & 1 \end{pmatrix}$

4) Robotic Rover State Space

Following the linearization, it is time to assemble the state space of the rover. Remember that the obtained state space is a simplified version. It only works well if the body slip angle is not very large ( $\beta \approx 0$ ). So if the body slip angle is very large, the state space would not be held anymore. It also only can work if the steering angle does not deviate much from a very small angle ( $\delta \approx 0$ ). If the rover steering angle is very large, the state space would not hold anymore: the rover would not be moving in a straight line, therefore, the system is would not be linear. Regardless of the limitations of the state space, let’s put everything together.

$\dot{\mathbf{x}} = A \mathbf{x} + B \mathbf{u}$

where:

$A = \begin{pmatrix} 0 & 0 & -v_0 \sin(\theta_0) & \cos(\theta_0) \\ 0 & 0 & v_0 \cos(\theta_0) & \sin(\theta_0) \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix}$

and

$B = \begin{pmatrix} -v_0 \sin(\theta_0) & 0 & 0 \\ v_0 \cos(\theta_0) & 0 & 0 \\ 0 & \frac{v_0}{L} & 0 \\ 0 & 0 & 1 \end{pmatrix}$

5) Robotic Rover LQR Control

Once we have the robotic rover state space, it is time to perform some meaningful motion control. For this purpose, let us leverage the control knowledge that we have learned in previous chapters. Among all the controllers, let us pick the LQR controller (explained in Chapter 13) for this purpose.

Recall that for LQR control, the Continuous-Time Algebraic Riccati Equation (CARE) equation is

$A^T P + P A - P B R^{-1} B^T P + Q = 0$

Using python function: scipy.linalg.solve_continuous_are ,
we can solve the matrix P. Note that scipy is the python package.

Similarly, lets recall the LQR gain matrix $K$ :

$K = R^{-1} B^T P$

We can use the python function K = np.linalg.inv(R) @ B.T @ P to calculate the gain matrix K. Note that np is the numpy package of python.

Given that we use the state cost matrix Q and R in the following forms.

$Q = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$

$R = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$

With python:

Q = np.diag([1, 1, 1, 1])  # State cost matrix Q
R = np.diag([1, 1, 1])     # Input cost matrix R

Note that np is the numpy package of the python.

We can solve for the gain matrix K easily. The results are shown in the following figure. Given the target point, with LQR, the rover is able to navigate itself to that target point.

Robotics Rover with LQR Control — Figure 16.2: The robotics rover trajectory control with LQR.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Robotics and Controls Engineering Copyright © by Hongbo Zhang; Elissa Ledoux; and Vishwas Bedekar is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.