14 Model Predictive Controller
Hongbo Zhang
1) Overview of Model Predictive Control
- x(k) is the state vector at time step k .
- u(k) is the control input vector.
- d(k) is the disturbance vector.
-
y(k) is the output vector.
- A, B, Bd, and C are matrices that define the system dynamics.
- w(k) and v(k) are process and measurement noise, respectively.
2) Using a Kalman Filter to Reduce Noise
(A) Prediction Step:
![]()
![]()
(B) Update Step:
![]()
![]()
![]()
3) Model Predictive Control (MPC) Modeling
![Rendered by QuickLaTeX.com \[J = \sum_{i=0}^{N-1} \left( (x(k+i) - x_{\text{ref}}(k+i))^T Q (x(k+i) - x_{\text{ref}}(k+i)) \right) + \lambda \sum_{i=0}^{N-1} \left( u(k+i)^T R u(k+i) \right)\]](https://mtsu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-36e4caa54b997a2f1dcab575f7076f04_l3.png)
subject to the following constraints:
![]()
![]()
![]()
![]()
where:
- N is the prediction horizon
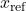 is the reference state.
is the reference state.- Q and R are the weighting matrices for the state and control input, respectively.
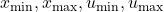 are the state constraints and the control inputs.
are the state constraints and the control inputs.
(1) First Example: MPC with Kalman Filter Modeling
Given the state space listed as follows, let’s define a simple system with:
![]()
The discrete state space is subject to the following constraints:
- Control input constraints:
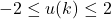
- State constraints:
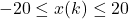
With the above parameters, we will solve the problem using MPC. Note that this example does not consider noises.
With the above formulation, we need to use a Kalman filter to estimate the state ![]() by observing the values of the measurements
by observing the values of the measurements ![]() .
.
The above equation can be easily formulated through the following MPC formulation:
![]()
The solution steps:
- Initialization: start with the initial state
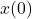 and the initial state estimate
and the initial state estimate 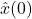
- Kalman Filter Update: For each step, at each time step k, update the state estimate using the Kalman filter.
- Prediction: For each step, predict future states using the state-space model and the updated state estimate.
- Optimization: Solve the optimization problem to find the optimal control inputs.
- Apply Control: Apply the first control input
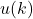 to the system.
to the system. - Update: Update the state
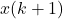 using the applied control input and repeat the process.
using the applied control input and repeat the process.
The solution code is shown below in part (3) Solutions
(2) Second Example: MPC with Kalman Filter Modeling
Given the same system with noises, the state space can presented as follows.
![]()
We’ll define the process noise covariance ![]() and measurement noise covariance
and measurement noise covariance ![]() as follows:
as follows:
![]()
For the noisy system condition, once the process noises and measurement noises are in existence in the system, the cost function should consider it as well. The noises are the process noise covariance ![]() and measurement noise covariance
and measurement noise covariance ![]() as follows:
as follows:
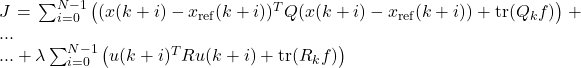
where:
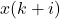 is the predicted state at time step
is the predicted state at time step 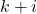
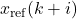 is the reference state at time step
is the reference state at time step 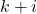
- Q is the state weighting matrix
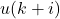 is the control input at time step
is the control input at time step 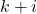
- R is the control input weighting matrix
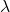 is a weighting factor for the control effort
is a weighting factor for the control effort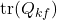 is the trace of the process noise covariance matrix
is the trace of the process noise covariance matrix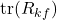 is the trace of the measurement noise covariance matrix
is the trace of the measurement noise covariance matrix
The solution code is shown below in part (3) Solutions
(3) Solutions
Solution to first example: The code used to implement the MPC system without noises is shown in below. More specifically, the given state space without noises can be presented as follows.
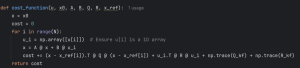
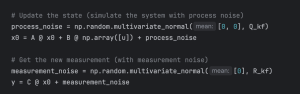
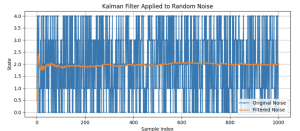
Now that the system has noises, a Kalman filter is needed to filter the noises from the system. The Kalman filter predicates the states, updates the error covariance matrix, and calculates the Kalman gain.
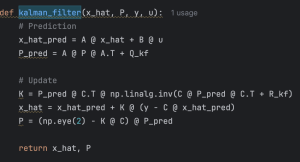
The new cost function considering the noises is then used to replace the original cost function. Note that, the new cost function includes Q, the process noise covariance, and R, the measurement noise covariance.

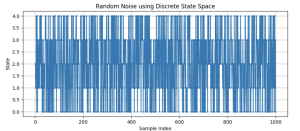
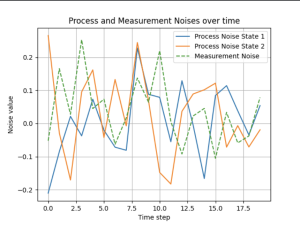
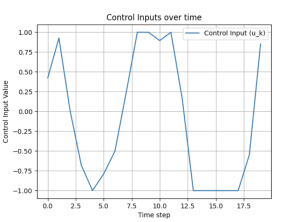
Following the process above, we can obtain the following state results. The two results correspond to the two different conditions where either no noises exist (Figure 14.7), or process and measurement noises are in existence (Figure 14.8).
Evidently, the results of the states and the input have both satisfied the constraints. Therefore, we can confidently say that the proposed MPC is effective in solving the state space while considering both process and measurement noises in the system.
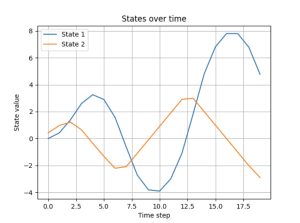
4) Class Engagement
Now you have learned the MPC theory, lets make summarization of the nature of the MPC controller. The key thing to implement MPC controller is to have optimal controller to solve the cost function a shown in below. Specifically, we use python package cvxpy to minimize the cost function.
![Rendered by QuickLaTeX.com \[J = \sum_{i=0}^{N-1} \left( (x(k+i) - x_{\text{ref}}(k+i))^T Q (x(k+i) - x_{\text{ref}}(k+i)) \right) + \lambda \sum_{i=0}^{N-1} \left( u(k+i)^T R u(k+i) \right)\]](https://mtsu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-36e4caa54b997a2f1dcab575f7076f04_l3.png)
Python Code:
cost += cvxpy.quad_form(x[:, t + 1], Q)
cost += cvxpy.quad_form(u[:, t], R)
The constrains needed to be satisfied is
![]()
[x[:, t + 1] == A @ x[:, t] + B @ u[:, t]]
————— The Key Code of MPC in Python ————–
for t in range(T):
cost += cvxpy.quad_form(x[:, t + 1], Q)
cost += cvxpy.quad_form(u[:, t], R)
constr += [x[:, t + 1] == A @ x[:, t] + B @ u[:, t]]
Other Constains
![]()
![]()
where:
Python Code:
constr += [x[:, 0] == x0[:, 0]]
The below is to solve it with cvxpy.Minimize function
prob = cvxpy.Problem(cvxpy.Minimize(cost), constr)
We will use the same class engagment example as shown in the LQR chapter. For this problem, an inverted pendulum sits on a cart moving along the x-axis direction shown in Figure 14.10. The inverted pendulum can move along the X and Y direction. It means the inverted pendulum can swing back and forth shown.
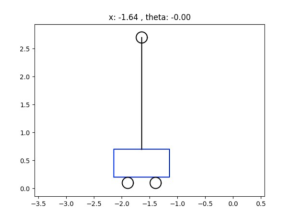
Figure 14.10 : Example of using Python to compute the LQR control gain K.
In order to control the inverted pendulum using LQR , we need to model the system. The followings show the process of the modeling
Through the derivation above, you can find the system state space as the following.
![Rendered by QuickLaTeX.com \[ \begin{bmatrix} \dot{x} \\ \ddot{x} \\ \dot{\theta} \\ \ddot{\theta} \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & -\frac{gm}{M} & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & \frac{g(M+m)}{lM} & 0 \end{bmatrix} \begin{bmatrix} x \\ \dot{x} \\ \theta \\ \dot{\theta} \end{bmatrix} + \begin{bmatrix} 0 \\ \frac{1}{M} \\ 0 \\ \frac{1}{lM} \end{bmatrix} F \]](https://mtsu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-58b61be6ee2cea4340e48926b6346484_l3.png)
Following running the code, results show that the use of LQR is able to stabilize the cart motion as shown in Figure 14.11. Specifically, when the cart is moving from one side to another, the inverted pendulum stays upright.

Figure 14.11: The results of running MPC python code showing that MPC is able to stablize the inverted pendulum on the moving cart.

