Full State Feedback Controller

Hongbo Zhang

15 Full State Feedback Controller

Hongbo Zhang

1) Overview of the Full State Feedback Controller

The Full State Feedback Controller, also called the pole placement approach, is a simple yet effective control method. In comparison to LQR and MPC control methods, full state feedback control is less computationally extensive. Therefore, it is a method used extensively for more deterministic control systems, where noises are not significant considerations of the controller.

$\newline$

The full state feedback control is based on the motivation that given any control system, poles are always important to deciding the control performance. As long as the poles of the control system are aligned with the expected pole locations, the control system is able to achieve the desired performance.

$\newline$

Fortunately, based on the user requirements, we know the overshoot and settling time information. With this information, we are able to determine the user desired poles. So, our goal is to come up a control design strategy to ensure the designed control system poles are able to match the user desired poles. We also call this method pole placement.

$\newline$

The state space diagrams of both open loop and closed loop systems are shown in the following figure. Through the figure, it is evident that the open-loop state space includes A, B, and C. In contrast, the closed loop control includes A, B, C, and -K. The control gain K provides feedback to each state among all the states x. We call this as full state feedback control. By comparing the two different diagrams, we can find that the only difference is the feedback matrix K. The focus of the full state feedback control is to calculate the feedback matrix K shown in Figure 15.1.

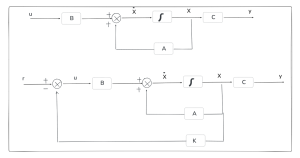
State space block diagram — Figure 15.1: The control block diagram of the open-loop and closed-loop control system.

Full state feedback control can be easily represented through flow diagrams. The flow diagrams corresponding to the block diagrams are shown in below. These diagrams assume a 3-state system, where $x = [x_1; x_2; x_3]$ . Similar to control block diagrams, flow diagrams show the relationships and interactions between the states, as in figures 15.2 and 15.3.

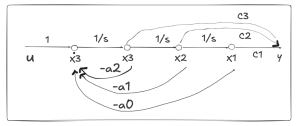
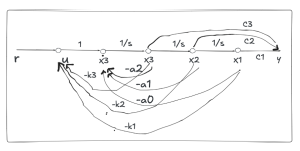
flow diagram of the state space. — Figure 15.2: The flow diagram of the open loop control.

2) Controllability and Observability

Prior to the discussion of the system control and attempting to control the system, it is important to have a good understanding of the system controllability and observability. It would be counterproductive to spend significant effort to model the system and try to design a controller for it without first confirming the controllability and observability of the system.

2.1) System Controllability

The system controllability is defined as follows. Given the control system below,

$\dot{x}(t) = A x(t) + B u(t)$

$y(t) = Cx(t) + Du(t)$

where $A$ is the system matrix, $B$ is the input matrix, $C$ is the output matrix, and $D$ is the feed-forward matrix. Based on the above state space definition, the controllability matrix $\mathcal{C}$ is defined as:

$\mathcal{C} = [B \ AB \ A^2B \ \cdots \ A^{n-1}B]$

Where $n$ is the number of states in the system.

$\newline$

The system controllability is defined when the determinant of the controllability matrix $\mathcal{C}$ is nonzero

$|\mathcal{C}| \neq 0$

or the controllability matrix rank is full rank.

$\text{rank}(\mathcal{C}) = full rank$

$\newline$

Let us use a simple example to illustrate the controllability of the system.

$\newline$

Example 1:

Given the system associated with the following A and B matrices:

$A = \begin{pmatrix} 0 & 1 \\ -2 & -3 \end{pmatrix}, \quad B = \begin{pmatrix} 0 \\ 1 \end{pmatrix}$

To determine if this system is controllable, we need to construct the controllability matrix $\mathcal{C}$ :

$\mathcal{C} = [B \ AB]$

First, we calculate $AB$ :

$AB = \begin{pmatrix} 0 & 1 \\ -2 & -3 \end{pmatrix} \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 1 \\ -3 \end{pmatrix}$

We know that the controllability matrix

$\mathcal{C} = [B \ AB]$

Therefore, the controllability matrix C can be written as

$\mathcal{C} = \begin{pmatrix} 0 & 1 \\ 1 & -3 \end{pmatrix}$

The determinate of the controllability matrix $|C|$ = -1. The rank of the controllability matrix is two: full rank. So we can conclude that the system is controllable.

Example 2:

Now let us introduce a second example of system controllability. The system of A and B is given below:

$A = \begin{pmatrix} 1 & 2 & 3 \\ 0 & -1 & 4 \\ 0 & 0 & -2 \end{pmatrix}, \quad B = \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}$

Therefore, the controllability matrix $\mathcal{C}$ is:

$\mathcal{C} = \begin{pmatrix} B & AB & A^2B \end{pmatrix}$

For this, we calculate $B$ $AB$ and $A^2B$ :

$AB = \begin{pmatrix} 1 & 2 & 3 \\ 0 & -1 & 4 \\ 0 & 0 & -2 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 4 \\ 4 \\ -2 \end{pmatrix}$

$A^2B = A(AB) = \begin{pmatrix} 1 & 2 & 3 \\ 0 & -1 & 4 \\ 0 & 0 & -2 \end{pmatrix} \begin{pmatrix} 4 \\ 4 \\ -2 \end{pmatrix} = \begin{pmatrix} 0 \\ 12 \\ 4 \end{pmatrix}$

$\newline$

With the above information, the controllability matrix $\mathcal{C}$ becomes:

$\mathcal{C} = \begin{pmatrix} B & AB & A^2B \end{pmatrix} = \begin{pmatrix} 1 & 4 & 0 \\ 0 & 4 & 12 \\ 1 & -2 & 4 \end{pmatrix}$

$\newline$

The controllability matrix $|C|$ determinant becomes

$\text{det}(\mathcal{C}) = 88$

$\newline$

The rank of controllability matrix $|C|$ becomes

$\text{rank}(\mathcal{C}) = 3$

$\newline$

As such, we conclude that the system is controllable.

2.2) System Observability

Similarly to controllability testing, observability testing is also begun from the system state space definition.

$\dot{x}(t) = Ax(t) + Bu(t)$

$y(t) = Cx(t) + Du(t)$

where $A$ is the system matrix, $B$ is the input matrix, $C$ is the output matrix, and $D$ is the feed-forward matrix.

Based on this definition, observability matrix $\mathcal{O}$ is defined as:

$\mathcal{O} = \begin{pmatrix} C \\ CA \\ CA^2 \\ \vdots \\ CA^{n-1} \end{pmatrix}$

where $n$ is the number of states.

Similar to the controllability matrix, the system is observable if the determinant of the observability matrix is nonzero:

$|\mathcal{O}| \neq 0$

or the observability matrix rank is full rank.

$\text{rank}(\mathcal{O}) = full rank$

Similarly, let us give some examples to better illustrate the observability check of the system.

Example 1:

Given A and B matrices as follows:

$A = \begin{pmatrix} 0 & 1 \\ -2 & -3 \end{pmatrix}, \quad C = \begin{pmatrix} 0 & 1\\ \end{pmatrix}$

The controllability matrix $\mathcal{C}$ is given by:

$\mathcal{O} = \begin{bmatrix} C \\ CA \end{bmatrix}$

First, we compute $CA$ :

$CA = \begin{bmatrix} 0 & 1 \end{bmatrix} \begin{bmatrix} 0 & 1 \\ -2 & -3 \end{bmatrix} = \begin{bmatrix} -2 & -3 \end{bmatrix}$

Therefore, the observability matrix is:

$\mathcal{O} = \begin{bmatrix} 0 & 1 \\ -2 & -3 \end{bmatrix}$

The determinant of the matrix C becomes

$\text{det}(\mathcal{O}) = 2$

As such, the system is observable.

Example 2:

Let us use the same 3×3 matrix as used in the controllability test to check the observability of the matrix.

$A = \begin{pmatrix} 1 & 2 & 3 \\ 0 & -1 & 4 \\ 0 & 0 & -2 \end{pmatrix}, \quad B = \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} ,\quad C = \begin{pmatrix} 1 & 0 & 1 \end{pmatrix}$

The observability matrix $\mathcal{O}$ can be calculated through $CA$ and $CA^2$ :

$CA = \begin{pmatrix} 1 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 2 & 3 \\ 0 & -1 & 4 \\ 0 & 0 & -2 \end{pmatrix} = \begin{pmatrix} 1 & 2 & 1 \end{pmatrix}$

$CA^2 = C(A^2) = \begin{pmatrix} 1 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 2 & 3 \\ 0 & -1 & 4 \\ 0 & 0 & -2 \end{pmatrix} \begin{pmatrix} 1 & 2 & 3 \\ 0 & -1 & 4 \\ 0 & 0 & -2 \end{pmatrix}$

$= \begin{pmatrix} 1 & 2 & 1 \end{pmatrix} \begin{pmatrix} 1 & 2 & 3 \\ 0 & -1 & 4 \\ 0 & 0 & -2 \end{pmatrix} = \begin{pmatrix} 1 & 2 & -5 \end{pmatrix}$

With $C$ , $CA$ and $CA^2$ , the observability matrix $\mathcal{O}$ becomes:

$\mathcal{O} = \begin{pmatrix} C \\ CA \\ CA^2 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 1 \\ 1 & 2 & 1 \\ 1 & 2 & -5 \end{pmatrix}$

The determinant of the $\text{det}(\mathcal{O})$

$\text{det}(\mathcal{O}) = -12$

The rank of the observability matrix $\mathcal{O}$ is full rank 3. As such, the system is observable.

3) Full State Feedback Control

3.1 Principle of Full State Feedback Control

The full state feedback control involves coefficient matching between the desired characteristics equation and the feedback control system characteristics equation to solve the feedback control gain K. In contrast to the linear quadratic regulator (LQR) and model predictive controller (MPC), the full state feedback controller is simpler to use and often yields the desired control gain K using more straightforward computation.

There are three major steps involved in calculation of the control gain K. The first step involves the calculation of the desired characteristics equation. The desired characteristics equation can be calculated using the damping ratio and natural frequency, which in turn can be calculated from overshoot and settling time, as shown in the first step of full state feedback control below.

Step 1: It should be noted that the dimension of the state space and the order of the desired characteristics equation correspond. For the two-by-two state space matrix, the order of the desired characteristics equation is two (second order). For higher dimensions of the state space, the order of the desired characteristics equation will increase. For this situation, we need to add augmented poles (S1 and S2 shown in Figure 4) for the first step of full state feedback control.

These augmented poles will be calculated using the system poles, which are the roots of the second order desired characteristics equation. The plant’s second order desired characteristics equation is written as:

$s^2 + 2\zeta\omega_n s + \omega_n^2 = 0$

Note that different values of $\zeta$ lead to different control system behaviors:
$\zeta = 0$ : Undamped system (pure oscillation).
$0 < \zeta < 1$ : Underdamped system (oscillatory response with decaying amplitude).
$\zeta = 1$ : Critically damped system (fastest response without oscillation).
$\zeta > 1$ : Overdamped system (slow response without oscillation).

The selection of augmented poles can be based on heuristics rules. For example, the real components of the augmented poles S1 and S2 can be 5 times or even 10 times larger than the roots of the above desired plant second order characteristics equation. Frequently, a trial-and-error approach is used to finalize the choice of S1 and S2. Of course, for the even higher dimensional state space, such as a 5×5 state space matrix, we will need three augmented poles: S1, S2, and S3 (2nd order system of 2 plant poles + 3 augmented poles = 5 poles total). Similarly, for the 6×6 state space matrix, we will need four augmented poles, S1, S2, S3, and S4. Together with two plant control system poles, this will make six poles to satisfy the total number of poles needed for a 6×6 state space matrix.

step-1 of the full state feedback controller — Figure 15.4: The first step of the full state feedback control

Step 2: The second step involves the calculation of the control system characteristics equation. The control system characteristics equation is

$det(SI-(A-BK))$

Where I is the identity matrix.

$[K_1, K_2, K_3... K_n ]$

Note that for phase variable form, the matrix A can be written as follows:

$\mathcal{A} = \begin{pmatrix} 0 & 1 & ... & 0 \\ 0 & 0 & ... & 0 \\ -a_0 & -a_1 & ... & -a_{n-1} \\ \end{pmatrix}$

$\mathcal{A-BK} = \begin{pmatrix} 0 & 1 & ... & 0 \\ 0 & 0 & ... & 0 \\ -(a_0+k_1) & -(a_1+k_2) & ... & -(a_{n-1}+k_n) \\ \end{pmatrix}$

For this condition, the characteristics equation (also the determinant of (SI- (A-BK)) becomes:

$det(SI-(A-BK)) = s^n + (a_{n-1} + k_n)s^{n-1}+ ... + (a_0+k_1)$

You can find two interesting behaviors for the determinant of the phase variable type state space SI – (A-BK). First, you can easily find that the value of the last row and last column of the A-BK matrix becomes the first coefficient of the determinant, whereas the value of the last row and first column becomes the last coefficient of the determinant. Second, it is also obvious that the sign of the coefficient is opposite as well between the last row of the A-BK matrix and the characteristic equation coefficients. However, this pattern only holds for the phase variable state space. Unfortunately, does not hold for other types of state space, such as control canonical and observer. For these, you must calculate the determinant in order to obtain the characteristic equation.

step of the full state feedback controller — Figure 15.6: The second step of the full state feedback control

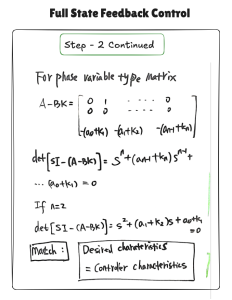
step-2 of the full state feedback controller — Figure 15.7: The second step (continued) of the full state feedback control

Step 3: Match Characteristic Equations to Solve K. Once the control system characteristics equation

$det(SI-(A-BK))$

is obtained, it is intuitive to match it with the desired control system characteristics equation to solve for the control gain K.

Control System Characteristics Equation = Desired Characteristics Equation

step-3 of the full state feedback controller — Figure 15.8: The third step of the full state feedback control

3.2 Case Study of the Full State Feedback Control

Given the system transfer function as follows, design a full state feedback controller to satisfy the following criteria: 15% overshoot, settling time of 0.5 seconds.

$H(s) = \frac{20}{(s+2)(s+3)}$

Step 1: Let us calculate the desired characteristics equation. We know that the overshoot is 15%.

$\%OS = 15\%$

We also know the system equation

$s^2 + 2\zeta\omega_n s + \omega_n^2 = 0$

From which, we can derive the system damping ratio equation:

$\zeta = \frac{ln(\%OS/100)}{\sqrt{\pi^2 + ln(\%OS/100)^2}}$

$\zeta = 0.52$

Similarly, we can also obtain the natural frequency equation

$\omega_n = \frac{4}{T_s \zeta }$

Where $T_s$ is the settling time.

$\omega_n = 15.47$

As such, the desired characteristic equation becomes:

$s^2 + 2\zeta\omega_n s + \omega_n^2 = 0$

Where

$\zeta = 0.52, \omega_n = 15.47$

It thus becomes:

$s^2 + 16 s + 239.5 = 0$

Step 2: Based on this transfer function, we can also obtain the following state space (matrices A and B are the same as in Example 1, above).

$A = \begin{bmatrix} -3 & 1 \\ 0 & -2 \end{bmatrix}$

$B = \begin{bmatrix} 0 \\ 1 \end{bmatrix}$

$C = \begin{bmatrix} 20 & 0 \end{bmatrix}$

$D = \begin{bmatrix} 0 \end{bmatrix}$

With the state space, we can easily draw the feedback flow diagram as shown below. With the flow diagram, we can find that there are two feedback gains K1 and K2. It is evident that all states (X1 and X2) of the flow diagram are associated with feedback gains (K1 and K2). As such, we call it full state feedback. The feedback flow diagram of the cascade type flow diagram is shown in Figure 15.9.

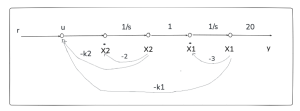
state space flow diagram — Figure 15.9: The feedback flow diagram of the cascade type flow diagram.

For the above flow diagram, the state space with feedback term is shown below. Note that only the A matrix has the feedback term; B, C, and D matrices do not have the feedback term.

$A - BK = \begin{bmatrix} -3 & 1 \\ -k_1 & -k_2-2 \end{bmatrix}$

$B = \begin{bmatrix} 0 \\ 1 \end{bmatrix}$

$C = \begin{bmatrix} 20 & 0 \end{bmatrix}$

$D = \begin{bmatrix} 0 \end{bmatrix}$

$\begin{bmatrix} \dot{x_1} \\ \dot{x_2} \end{bmatrix} = \begin{bmatrix} -3 & 1 \\ -k_1 & -k_2-2 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} + \begin{bmatrix} 0 \\ 1 \end{bmatrix}r$

$Y = \begin{bmatrix} 20 & 0 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}$

With the above feedback state space, we can obtain the following characteristics equation.

$det(SI-(A-BK)) = det\begin{bmatrix} \begin{bmatrix} s & 0\\ 0 & s \end{bmatrix} - \begin{bmatrix} -3 & 1 \\ -k_1 & -k_2-2 \end{bmatrix} \end{bmatrix} = det\begin{bmatrix} s+3 & -1 \\ k_1 & s+k_2+2 \end{bmatrix}$

$= (s+3)(s+k_2+2) +k_1$

$= s^2 + (k_2+5)s + 3k_2 + 6 + k_1$

Step 3: We know the desired characteristic equation is:

$s^2 + 16 s + 239.5 = 0$

The system characteristic equation is:

$0 = s^2 + (k_2+5)s + 3k_2 + 6 + k_1$

We therefore need to match coefficients between the two equations to solve K1 and K2. In doing so, we can obtain the following two equations to solve K1 and K2.

$k_2+ 5 = 16$