3 Forward Kinematics for Serial Manipulators
Elissa Ledoux
1) Basics of Forward Kinematics
Theory
Forward kinematics maps a robot’s joint positions to its end effector pose. It describes a manipulator’s motion irrespective of force and torque.
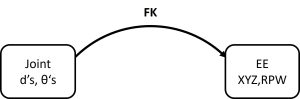
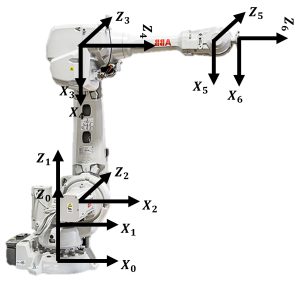
For simplicity, assume each joint in the chain has 1 DoF (or is two joints, etc.). For serial manipulators, place a coordinate frame on each joint, and number the joints in order from base to tip. The robot’s base is considered link 0, so the first joint (joint 1) drives link 1, joint 2 drives link 2, etc. The Z axis of each joint should indicate the axis of motion. An example robot (ABB IRB 6700) is shown below, with coordinate frames attached to each joint.
For a detailed introduction to forward kinematics, watch the Forward Kinematics Introduction video below.
Video: Forward Kinematics Intro (click link for closed caption version)
There are three common methods of solving for a robot’s forward kinematics equations. These are:
- Basic Method
- Denavit-Hartenberg (DH) Method
- Product of Exponentials (PE) Method
The basic method is used for simple robots, generally those that have three or fewer joints. The DH and PE methods are used for more complicated robots. Each section of this chapter will cover a different method of forward kinematics, with theory and examples.
The procedure for the basic method of forward kinematics is as follows:
- Put one coordinate frame on each link
- Find the link positions
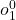 …
… 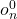
- Find the end effector frame orientation
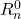
- Make the homogeneous transformation
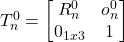
Examples
For a detailed explanation and example of forward kinematics for a two-link RR robot, see the video below.
Video: Forward Kinematics – Basic Method (click link for closed caption version)
Quick Quiz
2) Denavit-Hartenberg (DH) Method
Theory
The Denavit-Hartenberg (DH) method of forward kinematics uses a current-frame approach. Each transformation from one coordinate frame to another is represented by the product of four basic transformations:
- Rotation around current Z by angle
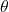 (“joint angle”)
(“joint angle”) - Translation along current Z by distance d (“link offset”)
- Translation along current X by distance a (“link length”)
- Rotation around current X by angle
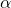 (“link twist”)
(“link twist”)
![Rendered by QuickLaTeX.com $T_i^{i-1} = [Rot_{z,\theta_i}] [Trans_{z,d_i}] [Trans_{x,a_i}] [Rot_{x,\alpha_i}] \\ \\ $ $T_i^{i-1} = \left\[ \begin{bmatrix} c_{\theta i} & -s_{\theta i}c_{\alpha i} & s_{\theta i}s_{\alpha i} & a_i c_{\theta i} \\ s_{\theta i} & c_{\theta i}c_{\alpha i} & -c_{\theta i}s_{\alpha i} & a_i s_{\theta i} \\ 0 & s_{\alpha i} & c_{\alpha i} & d_i\\ 0 & 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} R_i^{i-1} & o_i^{i-1} \\ 0_{1x3} & 1 \end{bmatrix} \right\]$](https://mtsu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-e835c69d6ff9d12d17166b01bdaf77b7_l3.png)
In layman’s terms, this transformation tells you the orientation and position coordinates of the robot’s current joint location relative to the previous one. This is illustrated in the following diagram:
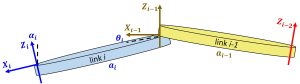
where the parameter assignments are:
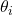 joint angle: angle from
joint angle: angle from 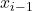 to
to 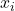 around
around 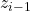
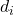 joint angle: angle from
joint angle: angle from 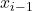 to
to 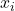 along
along 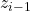
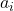 joint angle: angle from
joint angle: angle from 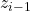 to
to 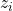 along
along 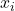
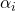 joint angle: angle from
joint angle: angle from 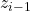 to
to 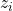 around
around 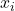
There are a few special cases for parameter assignment.
-
If
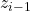 and
and 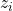 are not coplanar:
are not coplanar:
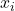 goes from
goes from 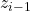 to
to 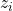 perpendicularly
perpendicularly -
If
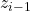 and
and 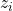 are parallel:
are parallel:
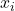 goes along link i-1
goes along link i-1 -
If
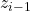 and
and 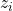 intersect:
intersect:
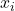 is perpendicular to that plane
is perpendicular to that plane
This theory is explained in the video below.
Video: Forward Kinematics – Denavit-Hartenberg (DH) Method (click link for closed caption version)
Once the parameter definitions and mathematical rules are understood, the procedure for actually determining the forward kinematics equations is:
- Identify joint axes
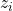 (1 per joint)
(1 per joint) - Attach coordinate frames (1 per link,
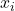 on link)
on link) - Identify and tabulate DH parameters
- Determine link transformations
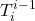
- Multiply all T‘s to obtain
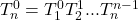
![]()
Keep in mind that while these transformations are extremely tedious and complicated to find by hand, they can be calculated very efficiently in Matlab by writing a function for the transformation matrix and using the DH parameters obtained in step 3 as inputs.
Examples
To demonstrate how to apply this theory to physical robots, two example videos are included. The first video below shows how to derive the DH parameters for a RPP cylindrical robot:
Video: FK Example – DH Method – RPP Cylindrical Robot (click link for closed caption version)
The following video shows how to derive the DH parameters for an RRR spherical wrist (the distal half of a standard 6-axis robot):
Video: FK Example – DH Method – RRR Spherical Wrist (click link for closed caption version)
Quick Quiz
3) Product of Exponentials Method
Theory
The Product of Exponentials (PE) method of forward kinematics uses the axis-angle formulation with ![]() instead of
instead of ![]() symbolizing the axis of rotation. For this method, math is done in the fixed (world) coordinate frame. The PE formula to find the transformation expressing the tip pose in the base frame is:
symbolizing the axis of rotation. For this method, math is done in the fixed (world) coordinate frame. The PE formula to find the transformation expressing the tip pose in the base frame is:
![]()
where ![]() is the robot’s home configuration (when all joint angles = 0) and
is the robot’s home configuration (when all joint angles = 0) and ![]() is the 4×4 transformation for link i. The subscripts 0 represents base frame and n represents tip frame. The squiggle
is the 4×4 transformation for link i. The subscripts 0 represents base frame and n represents tip frame. The squiggle ![]() is the Greek letter “xi” and is different than
is the Greek letter “xi” and is different than ![]() (“zeta”). In layman’s terms, this transformation tells you the orientation and position coordinates of the robot’s tip relative to its base frame.
(“zeta”). In layman’s terms, this transformation tells you the orientation and position coordinates of the robot’s tip relative to its base frame.
The procedure for implementing the product of exponentials method is as follows.
- Assign coordinate frames (base 0 and tip n), link velocities (
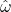 ‘s) and joint positions (d’s,
‘s) and joint positions (d’s, 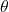 ‘s).
‘s). - Place p‘s (initial points)
- Find home configuration
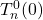
- Calculate twists (
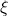 ‘s and
‘s and 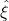 ‘s)
‘s) - Use the product of exponentials formula
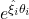 to build the base-to-tip transformation matrix
to build the base-to-tip transformation matrix
![]()
This theory is explained in the video below.
Video: Forward Kinematics – Product of Exponentials Method (click link for closed caption version)
The steps to implement the PE method of forward kinematics are detailed below:
Step 1: Assign coordinate frames (base 0 and tip n), link velocities (![]() ‘s) and joint positions (d’s,
‘s) and joint positions (d’s, ![]() ‘s).
‘s).
- Only assign coordinate frames for the links whose location in 3D space matters.
- If all that matters is the end effector location, only assign frames for base and tip.
- If simulating the entire robot (and all links need to be plotted), assign frames for all links.
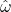 points along the Z axis (
points along the Z axis (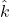 ) of the joint. It is a unit vector for revolute joints and 0 for prismatic joints since a prismatic joint has no angular velocity.
) of the joint. It is a unit vector for revolute joints and 0 for prismatic joints since a prismatic joint has no angular velocity.- d and
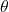 are positive in the +Z direction.
are positive in the +Z direction. - Remember that all coordinates are given in the world frame (fixed frame, base frame).
Step 2: Place p‘s (initial points)
- Place these anywhere along the joint’s Z axis.
- The most intuitive placement is on each joint frame origin.
- These values should be declared as constant parameters from the initial configuration, no need to account for joint motion.
Step 3: Find home configuration ![]()
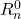 is a rotation you must determine from the relative orientations of the base and tip frames. Look at the two frames and see what rotations need to be done to go from base to tip. If the base and tip frames point in the same direction in this initial configuration, then
is a rotation you must determine from the relative orientations of the base and tip frames. Look at the two frames and see what rotations need to be done to go from base to tip. If the base and tip frames point in the same direction in this initial configuration, then 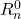 is just the identity matrix.
is just the identity matrix.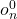 should be the same as p for the tip
should be the same as p for the tip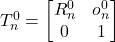
Step 4: Calculate twist coordinates (![]() ‘s) and twists (
‘s) and twists (![]() ‘s)
‘s)
- These represent joint velocities.
- For revolute joints: calculate these from
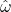 and p.
and p. - For prismatic joints: calculate these from v.
- Formulas for the angular velocity vectors, twist coordinates, and twists are shown in the table below:
| Prismatic Joints | Revolute Joints | |
| Angular velocity |
n/a | 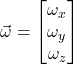 |
| Hatted ang vel |
n/a | 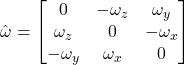 |
| Twist coordinates ( |
||
| Twists ( |
Keep in mind that sometimes 0 represents the matrix 0 depending on the elements to fill. The subscript i represents the joint number.
Step 5: Use the product of exponentials formula ![]() to build the base-to-tip transformation matrix
to build the base-to-tip transformation matrix
![]()
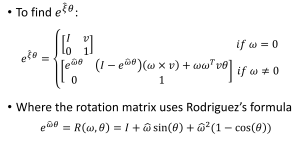
Keep in mind that while these calculations are extremely tedious and complicated to do by hand, they can be very efficiently simulated in Matlab by writing functions for steps 4 and 5 of the analysis and calling them in a script after defining and using the parameters obtained from steps 1-3.
Examples
These next few examples show how to perform forward kinematics analysis for serial robots using the Product of Exponentials method. The first video demonstrates an RPP cylindrical robot, the same robot from the example above using the DH method, but this time taking a new approach to analysis.
Video: FK Example – Prod Exp Method – RPP Cylindrical Robot (click link for closed caption version)
This next example covers PE FK analysis of a 6-DOF standard cobot arm.
Video: FK Example – Prod Exp Method – 6R UR Robot (click link for closed caption version)

