"

2 Rigid Body Transforms

Elissa Ledoux

1) Introduction to Rigid Body Transforms

Robots can be modeled as a combination of rigid bodies in 3D space.  The maximum degrees of freedom in 3D space is six: x/y/z position and roll/pitch/yaw orientation.  The combination of position and orientation is called a pose and is described by a mathematical matrix.  One transformation matrix is used per link of a robot to indicate pose, but rigid body transforms can also be used to represent points or vectors in different coordinate frames.  Uses of rigid body transforms include:

  • indicating coordinates of the same point or vector in two different frames
    example: location of a part to pick in the robot’s frame of reference versus the camera’s frame versus the operator’s frame
  • describing the motion of a point or vector from one pose to another
    example: moving a part from point A to point B
  • calculating forward kinematics
    example: pose of a robot’s tip relative to its base

If the difference between the new frame/point/vector and the old frame/point/vector is just a rotation, a 3×3 rotation matrix is used to relate the two.  If the difference includes a translation, a 4×4 homogeneous transformation matrix is used.  This chapter will address rotations first and transformations second.

Quick Quiz

2) Rotations

A rotation matrix is a 3×3 matrix that describes the relationship between two different frames of reference, a new frame versus an original frame.  For example, the matrix R_1^0 represents the orientation of the new frame 1 (subscript) relative to the original frame 0 (superscript).  Matrix R_0^1 would be the inverse (or transpose) of that, representing frame 0 with respect to frame 1.

The columns of a rotation matrix represent the unit coordinate axis vectors, where x is the first column, y is the second column, and z is the third column.  The video below explains the basics of rotation matrices, how they are derived, and how to describe a point in a new frame versus an old frame.

Video: Rotations – Basics (click link for closed-caption version).

The basic rotations around each unit vector are as follows:

Rotation about x axis:

    R_{x,\theta} = \left\[ \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos(\theta) & -sin(\theta) \\ 0 & sin(\theta) & cos(\theta) \\ \end{bmatrix} \right\]

Rotation about y axis:

    R_{y,\theta} = \left\[ \begin{bmatrix} cos(\theta) & 0 & sin(\theta)\\ 0 & 1 & 0 \\ -sin(\theta) & 0 & cos(\theta) \end{bmatrix} \right\]

Rotation about z axis:

    R_{z,\theta} = \left\[ \begin{bmatrix} cos(\theta) & -sin(\theta) & 0\\ sin(\theta) & cos(\theta) & 0\\ 0 & 0 & 1 \end{bmatrix} \right\]

To calculate a point in a new frame if the two frames and the original point are known, one would use the formula:

    \[p^1 = R_0^1 p^0 \]

where p^1 is the point (3×1 matrix) represented in the new frame (1), R_0^1 is the orientation (3×3 matrix) of the new frame (1) with respect to the old frame (0), and p^0 is the coordinates (3×1 matrix) of the point in the original frame.

The video below shows an example of how to mathematically calculate a rotation matrix, inverse rotation matrix, and point in new coordinate frame using numerical values and a real life application.

Video: Rotation Example (click link for closed caption version)

When two or more rotations are involved to go from the original frame to the final frame, i.e. a sequence of rotations is performed, this can be done in two different ways: current frame rotations versus fixed frame rotations.  Current frame rotations are done in the current frame, i.e. each rotation is done relative to the previous frame.  In this situation, the rotation matrices are post-multiplied, with each successive rotation multiplied on the right of the previous one.  Fixed frame rotations are done relative to the original frame.  In this case, the rotation matrices are pre-multiplied, with the new rotation multiplied before or on the left side of the previous one.  A detailed explanation and examples are given in the video below.

Video: Rotation Sequences (click link for closed caption version)

Euler’s rotation theorem says that the displacement of a rigid body with one point fixed is a rotation about an axis through that point.  To visualize this, imagine a pinwheel.  The pin is the fixed point, and the wheel turns about it.  Another example is a pendulum.  The top of the pendulum is pinned, and the bottom rotates around that point.

Rotations can be represented in multiple ways.  The most common way is the 3×3 rotation matrix explained above; however, it is not the only way.  Others include:

  • Roll-pitch-yaw: a sequence of three fixed-frame rotation matrices, 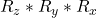R_z*R_y*R_x, most common in robotics and aviation
  • Euler angles: a sequence of any three current frame rotation matrices, not necessarily x, y, and z
  • Axis-angle: a 4-parameter set, one 3×1 unit vector 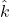\hat{k} representing the axis of rotation, and the angle of rotation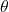 \theta
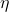  • Quaternion: another 4-parameter set, with a 3×1 unit vector \epsilon and a scalar \eta, used to avoid singularities

These representations and their mathematical formulas are explained in the video below along with examples.

Video: Rotation Representations (click link for closed caption version)

An additional example detailing how to calculate a single rotation matrix representing a roll-pitch-yaw orientation sequence is in the following video.

Video: Roll-Pitch-Yaw Rotation Example (click link for closed caption version)

Quick Quiz

3) Homogeneous Transformations

Chasle’s theorem says that the most general displacement of a rigid body is translation along an axis (d) and rotation about the same axis (R).  In this situation, the order of rotation versus translation does not matter because the rotation and translation are done with the same axis.  This is represented mathematically by a 4×4 homogeneous transformation matrix, which combines the 3×3 rotation matrix R with the 3×1 translation location d, and a bottom row of three zeros and a one:

    $T = \left\[ \begin{bmatrix} cos(\theta) & -sin(\theta) & 0 & x \\ sin(\theta) & cos(\theta) & 0 & y \\ 0 & 0 & 1 & z\\ 0 & 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} R_{3x3} & d_{3x1} \\ 0_{1x3} & 1 \end{bmatrix} \right\]$

If the motion is pure translation, the rotation matrix R is just the identity matrix.

Homogeneous transformations can represent:

  • Relative position and orientation between coordinate frames
  • Passive transformation of a point or vector into a new coordinate frame
  • Active transformation of a point or vector in a fixed reference frame

To express a point p in a new frame using transformations if the position of the point has changed, the formula is similar to the one for rotations:

    \[p^1 = T_0^1 p^0 \]

where p^1 is the point (4×1 matrix) represented in the new frame (1), T_0^1 is the orientation (4×4 matrix) of the new frame (1) with respect to the old frame (0), and p^0 is the coordinates (4×1 matrix) of the point in the original frame.  In order to make the point a 4×1 matrix when it only has three coordinates, augment it with a one: p = [x; y; z; 1].  Doing this preserves the effect of the original position, or fourth column, of the transformation matrix. Vectors should be augmented with a zero because they are location independent (directional only).

In contrast to rotation sequences, which can be done in fixed or current frames, homogeneous transformations are just done in current frames (each frame relative to the one before it).  For a standard six-axis industrial robot, for example, the transformation relating the tip of the robot (frame 6) relative to the base is:

    \[T_6^0 = T_1^0 T_2^1 T_3^2 T_4^3 T_5^4 T_6^5 \]

A second difference between transformations and rotations is the method of finding the inverse.  Whereas for a rotation, the inverse is simply the transpose (swap rows and columns), for a transformation, the formula is more complicated:

    $T^{-1} = \left\[ \begin{bmatrix} R^T & -R^T d \\ 0 & 1 \end{bmatrix} \; where \;\; T^b_a = (T^a_b)^{-1} \right\]$

An introduction to the theory of homogeneous transformations is provided in the following video:

Video: Homogeneous Transformations (click link for closed caption version)

The following video provides a detailed example of using a homogeneous transformation matrix to calculate the pose of a point in a new frame relative to the original frame, using the example of a space ship shooting a missile at a target while moving.

Video: Transformation Example (click link for closed caption version)

Quick Quiz

——————EXAMPLES————————————-

At first, we sample f(x) in the N (N is odd) equidistant points around x^*:

    \[ f_k = f(x_k),\: x_k = x^*+kh,\: k=-\frac{N-1}{2},\dots,\frac{N-1}{2} \]

where h is some step.
Then we interpolate points \{(x_k,f_k)\} by polynomial

(1)   \begin{equation*} P_{N-1}(x)=\sum_{j=0}^{N-1}{a_jx^j} \end{equation*}

    \begin{bmatrix} c & -s & 0 & x\\ s & c & 0 & y\\ 0 & 0 & 1 & z\\ 0 & 0 & 0 & 1 \end{bmatrix} [\latex] [latex] Rotation $R_0^1 = \left\[ \begin{bmatrix} cos(\theta) & -sin(\theta) & 0\\ sin(\theta) & cos(\theta) & 0\\ 0 & 0 & 1 \end{bmatrix} \right\]$

    Transformation $T_0^1 = \left\[ \begin{bmatrix} cos(\theta) & -sin(\theta) & 0 & x \\ sin(\theta) & cos(\theta) & 0 & y \\ 0 & 0 & 1 & z\\ 0 & 0 & 0 & 1 \end{bmatrix} \right\]$

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Robotics and Controls Engineering Copyright © by Hongbo Zhang; Elissa Ledoux; and Vishwas Bedekar is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book