11 State Space Modeling
Hongbo Zhang
1) Modeling of Mechanical System State Space
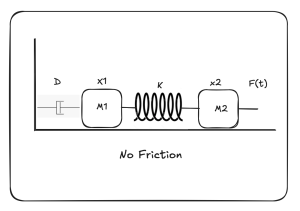
In this example, the image shows a mechanical system with two masses, M1 and M2, shown in Figure 11.1. The two masses are connected to a spring and damper. An external force F(t) is imposed on the system. Based on the system, there are two states, X1 and X2, shown in Figure 11.2. The two states are correlated. Object 1 is associated with position X1, and object 2 is associated with position X2. The modeling process starts with analysis of M1 and M2. M1 is associated with two different motions: X1 on the left, and both X1 and X2 on the right. This is similarly true for M2, which is associated with X1 and X2 on the left. However, it is associated with F(t) on the right.

In this example, it is easy to ignore the motion associated with the object. For example, mass M1 is associated with X1 and X2 of the spring motion located on the right side of M1. In this case, spring motion X1 is positive and X2 is negative. On the other hand, M2 motion is denoted as X2. On the left side of the M2, the spring is associated with the motions X2 and X1. Figure 11.2 shows these two different motions.
The state space of the mechanical system shown in Figure 11.2 can be derived through the following steps. First, conduct the variable replacement as shown in Figure 11.3. The purpose of the variable replacement is to reduce the second order equation to two first order equations.
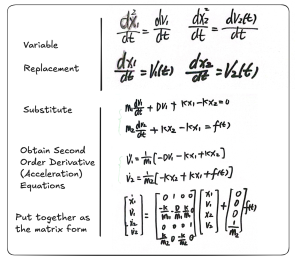
For this:
(1) ![]()
Therefore the second order derivative of the equation is
(2) ![]()
With these two variable replacements, we can easily substitute ![]() back into the system dynamics equations to obtain the substituted system equations.
back into the system dynamics equations to obtain the substituted system equations.
(3) ![]()
(4) ![]()
Finally, we can write the state space format to represent these equations in the state space format shown in Figure 11.3 above.
2) Modeling of Electrical System State Space
Following the modeling of the mechanical system, it is time to consider modeling of an electrical system. In order to model an electrical system, it is important to understand the relationships between current, voltage, and charge. These relationships are important for us to be able to model capacitors, inductors, and resistors in a circuit. The relationships of current, voltage, and charge for capacitors, inductors, and resistors are shown in Figure 11.4.

In Figure 11.4, you can find a strong pattern showing an inverse relationship between capacitor current and voltage equations. The capacitor current equation is a derivative equation. However, its voltage equation is an integral equation. Similarly, the inductor current equation is a derivative equation, while the voltage equation is an integral equation. By understanding the patterns, it becomes easy for us to use these equations effectively.
To be most effective in remembering or using the equations, start by remembering the capacitor charge equation. It is a simple equation: ![]() , where
, where ![]() . It shows that a capacitor behaves similarly to a battery. It accepts a charge from a power source. The voltage is proportional to the charge on the capacitor. On the other hand, charge is the result of the continuous accumulation of current to the capacitor. These two equations are the most fundamental equations in an electrical circuit. These two equations are located at the top right of Figure 4. Understanding these two equations will help you understand the other equations in Figure 11.4.
. It shows that a capacitor behaves similarly to a battery. It accepts a charge from a power source. The voltage is proportional to the charge on the capacitor. On the other hand, charge is the result of the continuous accumulation of current to the capacitor. These two equations are the most fundamental equations in an electrical circuit. These two equations are located at the top right of Figure 4. Understanding these two equations will help you understand the other equations in Figure 11.4.
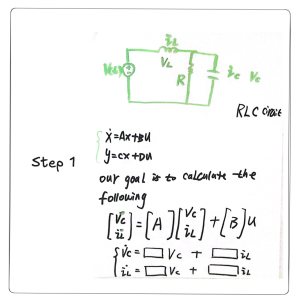
The first example of the circuit’s state space is shown in Figure 11.5. This example demonstrates a typical RLC circuit. In this example, the resistor and capacitor are in parallel. An inductor is in series with the capacitor and resistor lines. The question asks us to find the state space consisting of two states X1 = ![]() and X2 =
and X2 = ![]() . The output Y is
. The output Y is ![]() .
.
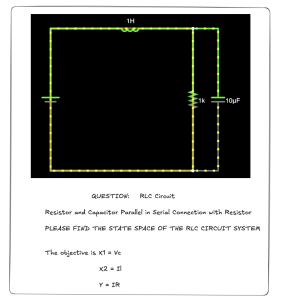
To solve the state space of an electrical circuit problem, we need to follow the following three steps.
Step 1: Define the goal. The goal is to find the state space equations for the system. By defining the state space, we can identify the “good” variables, which are the state space variables.
Step 2: Replace “bad” variables with “good” variables. Here, “bad” variables are the variables irrelevant to the state space. We need to replace these “bad” variables irrelevant to the state space with the “good” variables relevant to the state space.
Step 3: Confirm the state space. Following the replacement of “bad” variables with “good” variables, the state space will be obtained.
For this example, we need to follow these specific three steps.
Step 1 (Figure 11.6): The example of the RLC state space starts by understanding the target of the state space. The target of the state space is a two-by-two matrix. This two-by-two matrix essentially consists of two equations. These two equations are functions of the ![]() ,
, ![]() , and input U The input U here is
, and input U The input U here is ![]() . As such, step 1 is to understand the targeted state space. Once we understand the targeted state space, we start step 2.
. As such, step 1 is to understand the targeted state space. Once we understand the targeted state space, we start step 2.
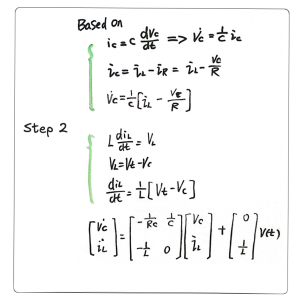
Step 2 (Figure 11.7): The key idea of step 2 is to replace “bad” variables with “good” variables. Step 2 starts by listing ![]() and
and ![]() . It should be noted that for
. It should be noted that for ![]() , there is a “bad” variable
, there is a “bad” variable ![]() . We can easily replace this “bad” variable with
. We can easily replace this “bad” variable with ![]() and R, which are both “good” variables. Similarly, for
and R, which are both “good” variables. Similarly, for ![]() , there is a “bad” variable,
, there is a “bad” variable, ![]() . However,
. However, ![]() can be replaced by the “good” variables
can be replaced by the “good” variables ![]() and
and ![]() .
.
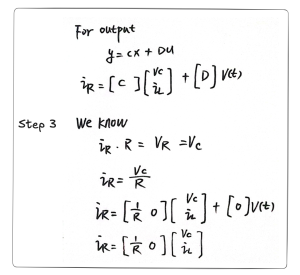
Step 3 (Figure 11.8): Following the replacement of the “bad” variables with “good” variables, we can obtain the targeted state space A and B matrices. Through step 3, we also can obtain the C and D matrices. To calculate the C and D matrices, the Y value must be calculated. Y is ![]() . Similarly, for calculation of
. Similarly, for calculation of ![]() , the “bad” variable
, the “bad” variable ![]() can be replaced by the “good” variables
can be replaced by the “good” variables ![]() and R. Through the replacement, the C and D matrices will be obtained.
and R. Through the replacement, the C and D matrices will be obtained.