10 Introduction to State Space
Hongbo Zhang
1) State Space
The state space is an important representation of the control system transfer function. The state space includes four different matrices: A, B, C, and D. The A matrix is the system matrix, which represents the dynamics of the underlying system. B is the input matrix, which represents the input(s) to the system. C is the output matrix, representing the output(s) for the system. Finally, D is the feedforward matrix for the system. The system of equations for the state space is as follows:
(1) ![]()
(2) ![]()
State space can be used to describe nearly any kind of control system including mechanical, electrical, pneumatic, and fluidic systems. Among all these systems, mechanical and electrical systems are the most typical systems to be modeled for the purpose of control operations. In contrast to the transfer function based modeling approach, the state space based modeling approach is able to capture the underlying states of the system (such as velocity and not just position), therefore making it easier to understand the system.
In the following example of the B matrix, it shows the three possible inputs. Note that the inputs for a mechanical system can refers to external forces or torques imposed on the mechanical system. The dimension of the B matrix is three, because it has three rows. This indicates that there could be up to three external forces or torques imposed on the system. If the underlying system is an electrical system, it then indicates that there could be three voltage or current sources.
(3) ![]()
A zero element in the B matrix indicates that regardless of the magnitude of the inputs, the input will not influence the system dynamics. The number of zeros are important to decide the controllability of the control system. Too many zeros in the B matrix will lead more difficulties in controlling the underlying system.
(4) ![]()
The C matrix is the output matrix. The output matrix elements indicate the output of the system. Please note that for a single input and single output (SISO) system, typically the C matrix is one column only. On the other hand, for multiple input and output (MIMO) system, if there are two outputs, the C matrix will be two columns.
(5) ![]()
Similar to the input matrix, the output matrix is also used to determine whether the states can impact the output, which is also known as observability of the system. If the C matrix has multiple elements as zero, it shows the likelihood of poor system observerability.
(6) ![]()
The disadvantages of the state space system are that it is not very straightforward to visualize the zeros, poles, and damping mechanisms. In comparison, it becomes much easier for transfer function based modeling approach to calculate and visualize the zeros, poles, and damping mechanisms. However, such disadvantages may not be a big problem for many systems once the initial system transfer functions have been determined. As matter of fact, most modern control systems tend to directly model the system using state space, and use state space to then calculate the transfer functions and the related zeros, poles, and damping mechanisms.
2) Flow Diagrams
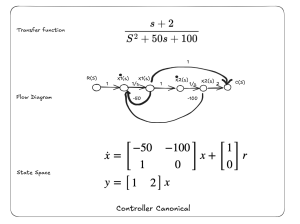
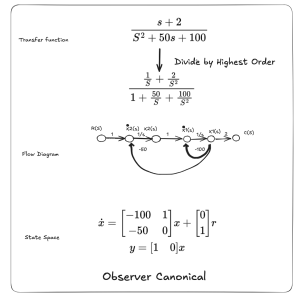
The flow diagram is an excellent visual representation of the control system. The flow diagram provides the ability to visualize the states of the system. It is also able to provide visualization for the feedback gains and feedforward gains. Visualizing the feedback and feedforward gains is helpful to understanding the system and design basis. The flow diagram also show the relationship between the states of the of the system. It is thus convenient to understand the states of the system. With a flow diagram, it is also possible to understand the stages being used to provide feedback, and visualize the state accepting the state feedback, thus understanding the beginning and ending of the states’ feedback. Similarly, it is also possible to understand the origin of the feed forward for the states and the associated gains.
The following image shows a simple example of a flow diagram in Figure 1. It consists of four different nodes. The four nodes are connected with three different links. The first node is the input R(s) to the system. The last node is the output C(s) of the system. In the system, x1(s) and sx1(s) are connected using a link with weight of 1/s.
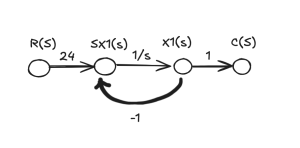
The way a flow diagram works is analogous to a warehouse to accepting and dispatching supplies. For example, the SX1(s) node will accept the incoming supply from R(s), and the 24 above the link indicates the weight of the supply. Similarly, x1(s) will supply a negative weight -1,. So the relationships are: SX1(s) = 24R(s) – X1(s), X1(s) = 1/s * SX1(s), C(s) = X1(s).
| Flow Diagram Name | Flow Diagram Properties | State Space |
| Phase Variable | The feedback terms (-50, -100) are in the feedback of the flow diagram. | The last row are the feedback gains (-50, -100) |
| Parallel | The feedback terms are in the feedback of the flow diagram. (-50, -100) | The diagonal elements are the feedback gains (-50, -100) |
| Cascade | The feedback terms are in the feedback of the flow diagram. (-50, -100) | The diagonal elements are the feedback gains (-50, -100) |
| Controller Canonical | The feedback terms are in the feedback of the flow diagram. (-50, -100) | The first row elements are the feedback gains (-50, -100) |
| Observer Canonical | The feedback terms are in the feedback of the flow diagram. (-50, -100) | The first column elements are the feedback gains (-50, -100) |
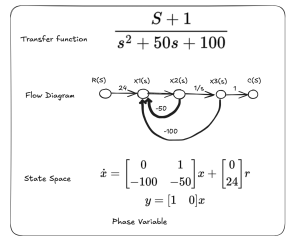
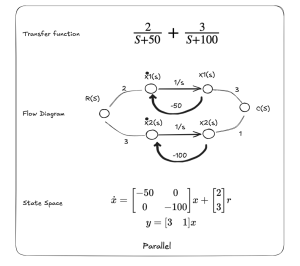
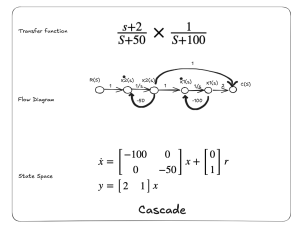
3) Class Engagement
(1) Given the following transfer function, please derive the state space and draw a flow diagram in phase variable format.
(7) ![]()
References
- Norman S Nise. Control systems engineering. John Wiley & Sons, 2020

