13 Linear Quadratic Controller
Hongbo Zhang
1) Motivation for the Linear Quadratic Controller
The Linear Quadratic Controller (LQR) and the Model Predicative Controller (MPC) are classical optimal controllers. They are effective and efficient in controlling linear systems. Both of them have been proven by theoretical and real-world control applications. It has been shown that the two controllers offer the best performance for real-world control systems.
LQR needs to work in the discrete state space because it is required to optimize the control function. So before we discuss the LQR controller, we need to first convert the state space to the discrete state space as shown in Figure 13.1. Why do we need to convert continuous state space to discrete state space? The basic idea is to be able to optimize the solution in the discrete state space domain. The discrete values of the solution to the state space allows one to optimize the controller.

![Rendered by QuickLaTeX.com x[k+1]= Ax[k] + Bu[k]](https://mtsu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-2a7b5d6bf82163f10722b0ae0748cca5_l3.png) .
.The discrete state space example shows that iterations are needed for the computation and the optimization of state space. The optimization of discrete state space is well illustrated in the previous chapter. In this current chapter, we will use another simpler example to better illustrate the importance of understanding the numerical computation of the state space.
The following example shows an example of discrete state space:
![]()
Where
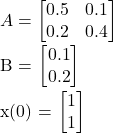
The state space will be iterated until the solution converges as shown in Figure 13.2. It is shown that following 22 iterations, the x value converges, yielding the value of
![]()

![Rendered by QuickLaTeX.com x[k+1]= Ax[k] + Bu[k]](https://mtsu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-2a7b5d6bf82163f10722b0ae0748cca5_l3.png) .
.With this example, you may wonder how we can use state space for a meaningful control task. Now, it is evident that the state space is not only an equation; rather, it it actually corresponds to a solution. It means that given a state space with ![]() and
and ![]() matrices, we can find the solution for the system of equations. Such a property naturally inspires us to use the discrete state space to find the control gain function to ensure the solution results in the desired values. By doing this, we can utilize the state space domain for meaningful control.
matrices, we can find the solution for the system of equations. Such a property naturally inspires us to use the discrete state space to find the control gain function to ensure the solution results in the desired values. By doing this, we can utilize the state space domain for meaningful control.
Now, we are not the only ones who have thought about this. As early as the 1950s, engineers have been inspired to adopt the state space techniques for solving difficult control problems. The development of the Linear Quadratic Controller (LQR) was heavily influenced by the work on dynamic programming by Richard Bellman and the optimal control theory by Lev Pontryagin. The optimal control law and the Linear Quadratic Controller have significant applications and are thus worth of our attention and investigation to learn how to use them to solve real-world control problems.
2) Overview of the Linear Quadratic Controller
2.1) Fundamentals of the Linear Quadratic Controller
The Linear Quadratic Controller is inspired by the optimal control law. Optimal control theory believes it is important to formulate a control problem as an optimization problem, where a cost function will guide the process to solve for the best solution of the underlying control problems. Rudolf Kalman played a significant role in determining an approach to formulate the LQR using optimal control theory. He proposed the use of the Riccati equation to practically solve the LQR problem. Specifically, the Riccati equation can compute the optimal feedback gains that minimize a quadratic cost function. The quadratic cost function helps achieve the goal of the control, which is to ensure that a state converges to the desired state with minimal overshoot while ensuring that the control command to the actuator is not excessively large. As we know, a large control input to motors will damage the motors. Therefore, the optimization function needs to consider the optimization of both state and input variables.
LQR controllers are very robust for real-world applications and often able to stabilize systems with guaranteed specifications and performance. Such properties have made it widely used in various engineering applications, including aerospace, robotics, and industrial automation.

(1) ![]()
where:
Q is a positive semi-definite cost matrix. The goal is to make ![]() always greater than or equal to zero regardless of negative values appearing in the X state matrix.
always greater than or equal to zero regardless of negative values appearing in the X state matrix.
R is a positive definite control cost matrix. It means ![]() is always greater than zero regardless of negative values appearing in the X state matrix.
is always greater than zero regardless of negative values appearing in the X state matrix.
Among this cost objective function, Q and R are two the most important variables used to achieve LQR control. An example of a semi-definite state cost matrix Q is:
![Rendered by QuickLaTeX.com \[Q = \begin{bmatrix} 2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1 & 2 \end{bmatrix}\]](https://mtsu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-b68e8af361d51dfecca639541d630616_l3.png)
This matrix is symmetric and positive semi-definite, meaning that for any non-zero vector x, the quadratic form
![]()
We should note that it is possible to have negative elements in the Q matrix. Such negative elements have a physical meaning. For example, for a mechanical system, the negative values in the Q matrix can represents damping effects or forces that act in opposition to the motion of the system. In electrical circuits, the negative elements represent resistances or impedances of the circuit.
Similarly, R, the control cost matrix, is also important. A representative control cost matrix R is as follows.
![]()
The goal of the matrix R is to ensure
![]()
In contrast to the Q matrix, the R matrix needs to be symmetric and positive. Therefore, there are never negative terms in the R matrix.
It is important to note that the selection of values for the Q and R matrices are important for LQR. Here are practical guidelines for the selection of Q and R.
Note 1: The goal of the Q matrix is to penalize the control states, so it is weighted accordingly. Higher values in the Q matrix correspond to states that you want to keep small. This means that for a given state, if you want to minimize the difference between the actual state and the desired state for a particular state, you can simply assign a larger corresponding weight to that state in the corresponding element of Q.
The design should be initiated using just the diagonal elements of the Q matrix and then expanding to use the non-diagonal elements if necessary. Using negative values is feasible if the corresponding state has damping and resistance associated with it.
Note 2: The goal of the R matrix is to penalize the control inputs, so the elements are weighted accordingly. Higher values in the R matrix correspond to higher penalties on the control inputs, which can help to prevent excessive control inputs.
Similar to the Q matrix, the choice of R matrix weight elements should also start with the diagonal elements of the R matrix. Once the diagonal elements are confirmed, one can consider using the non diagonal elements.
Note 3: Bryson’s rule is often used to select the values of the Q and R matrices. The general guideline based on Bryson’s rule is to set
![]()
![]()
Note 4: The selection of Q and R matrices needs to be performed in an iterative fashion. Start with initial values and iteratively choose other values until the states and control inputs meet the control design goal.
3) Control Gain Computation of the Linear Quadratic Controller
Another goal of the LQR is to obtain the control gain. The LQR control gain is denoted as ![]() . The relationship between control input, state, and LQR control gain
. The relationship between control input, state, and LQR control gain ![]() is described below. Please note that we need to use negative (
is described below. Please note that we need to use negative (![]() ) here for a negative feedback system.
) here for a negative feedback system.
(2) ![]()
To solve for the LQR control gain (feedback gain) ![]() , we need to follow a few steps introduced below:
, we need to follow a few steps introduced below:
Step 1 to Compute ![]() : To solve for the feedback gain K, we need introduce the Bellman equation. The Bellman equation was born from research dating back to the 1950s. The Bellman equation is based on Bellman’s principle of optimality. The principle of optimality emphasizes the use of state space to solve an optimization problem. The optimization policy states that regardless of the initial state and decision, the following decisions must constitute an optimal policy with respect to the state resulting from the first decision. (Each current decision must be chosen to optimize the remaining problem regardless of what was chosen for previous states.)
: To solve for the feedback gain K, we need introduce the Bellman equation. The Bellman equation was born from research dating back to the 1950s. The Bellman equation is based on Bellman’s principle of optimality. The principle of optimality emphasizes the use of state space to solve an optimization problem. The optimization policy states that regardless of the initial state and decision, the following decisions must constitute an optimal policy with respect to the state resulting from the first decision. (Each current decision must be chosen to optimize the remaining problem regardless of what was chosen for previous states.)
Specifically, the Bellman equation starts by introducing the “value function” ![]() , also known as the “cost-to-go function”.
, also known as the “cost-to-go function”.
(3) ![]()
Based on the Bellman equation optimality principle, it states that the optimal policy from any state ![]() must minimize the immediate cost plus the cost-to-go from the next state. For the LQR problem, this is written as:
must minimize the immediate cost plus the cost-to-go from the next state. For the LQR problem, this is written as:
(4) ![]()
(5) ![]()
As such, ![]() representing the cost-to-go from the next state
representing the cost-to-go from the next state ![]() can be represented as
can be represented as
(6) ![]()
We also know that
(7) ![]()
Hence, the Bellman equation for the discrete-time LQR problem is written as:
(8) ![]()
where ![]() is the value function representing the minimum cost-to-go from state
is the value function representing the minimum cost-to-go from state ![]() .
.
Step 2 to Compute ![]() : It is typically safe to assume that the value function is of a positive quadratic form (because a positive quadratic function has a global minimum). The quadratic form of the
: It is typically safe to assume that the value function is of a positive quadratic form (because a positive quadratic function has a global minimum). The quadratic form of the ![]() is:
is:
(9) ![]()
where ![]() is a symmetric positive semi-definite matrix. So basically P is the positive (+) coefficient, and
is a symmetric positive semi-definite matrix. So basically P is the positive (+) coefficient, and ![]() is squared, thus you have a positive quadratic.
is squared, thus you have a positive quadratic.
Combining the two equations above, substitute the quadratic form into the Bellman equation, we can obtain the following equation
(10) ![]()
Now, we know this Bellman equation:
![]()
We can expand the terms inside the minimization:
![]()
Subsequently, we can group the terms involving u :
![]()
To find the optimal control matrix u, take the derivative with respect to u and set it equal to zero:
![]()
This yields:
![]()
Based on the above equation, we can find the input u that optimizes the control law. In order to obtain the optimal control input ![]() , we can take the derivative with respect to
, we can take the derivative with respect to ![]() and set it equal to zero:
and set it equal to zero:
(11) ![]()
Finally, solve for ![]() . This is the most important step for obtaining the control input
. This is the most important step for obtaining the control input ![]() !!
!!
(12) ![]()
We also know that control the input is equal to
![]()
Therefore, the control gain ![]() becomes
becomes
(13) ![]()
Step 3 to Compute ![]() : In order to calculate the LQR control gain
: In order to calculate the LQR control gain ![]() , we need to first calculate the P matrix. In order to solve for P, we must rely on the Bellman equation again. For now, we need to substitute
, we need to first calculate the P matrix. In order to solve for P, we must rely on the Bellman equation again. For now, we need to substitute ![]() , so we can obtain
, so we can obtain
(14) ![]()
Rewrite the equation in terms of the quadratic form:
![]()
For the equation to hold for all ![]() , the matrix inside the quadratic form must equal zero:
, the matrix inside the quadratic form must equal zero:
![]()
Simplify the term using the matrix inverse: ![]()
Using the Woodbury matrix identity, we can simplify this term. The Woodbury identity states:
![]()
However, in many control theory contexts, we assume R is invertible and simplify directly:
![]()
Substitute the simplified inverse term back into the equation to obtain the discrete-time algebraic Riccati equation (DARE) :
![]()
With the substitution of
![]()
we are able to rearrange to obtain the discrete-time algebraic Riccati equation (DARE):
(15) ![]()
Step 4 to Compute K: In order to solve for K, we must first solve for P. In the DARE equation, it is difficult to isolate P. P cannot be solved for easily, as shown in the following DARE equation:
(16) ![]()
However, it is still feasible for us to solve this equation using iterative numerical methods. One common method involves the use of the Schur method or the Newton-Kleinman iteration method. These methods iteratively update the matrix P until convergence.
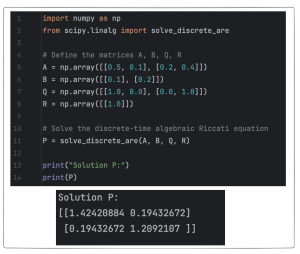
The Python SciPy package has built-in functions to solve the DARE. Specifically, the package below is able to do this work: scipy.linalg.solve_discrete_are function from the SciPy library. Example of using Python to compute P and K are shown in Figures 13.4 and 13.5.
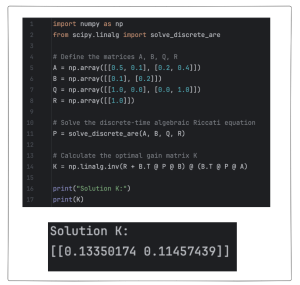
4) Class Engagement
There are a few interesting example showing you the implementation of the LQR involving Arduino. Among them, the use of LQR to control the inverted pendulum is an interesting application.
For this problem, an inverted pendulum sits on a cart moving along the x-axis direction. The inverted pendulum can move along the X and Y direction. It means the inverted pendulum can swing back and forth shown.
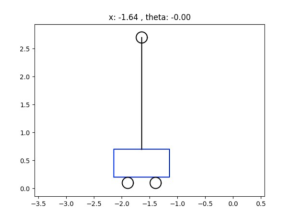
Figure 13.6: Example of using Python to compute the LQR control gain K.
In order to control the inverted pendulum using LQR , we need to model the system. The followings show the process of the modeling
Through the derivation above, you can find the system state space as the following.
![Rendered by QuickLaTeX.com \[ \begin{bmatrix} \dot{x} \\ \ddot{x} \\ \dot{\theta} \\ \ddot{\theta} \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & -\frac{gm}{M} & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & \frac{g(M+m)}{lM} & 0 \end{bmatrix} \begin{bmatrix} x \\ \dot{x} \\ \theta \\ \dot{\theta} \end{bmatrix} + \begin{bmatrix} 0 \\ \frac{1}{M} \\ 0 \\ \frac{1}{lM} \end{bmatrix} F \]](https://mtsu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-58b61be6ee2cea4340e48926b6346484_l3.png)
With this state space modeling, it becomes feasible for us to control the inverted pendulum using LQR with the python code as shown in below
Following running the code, results show that the use of LQR is able to stabilize the cart motion as shown in Figure 13.7. Specifically, when the cart is moving from one side to another, the inverted pendulum stays upright.

Figure 13.7:
Figure 13.7: The results of running MPC python code showing that MPC is able to stabilize the inverted pendulum on the moving cart.

